List Iteration, List Splicing and List Comprehension [alias, Set Builder Notation in code format]

• 1) Everything is object based. Even basic data types like (int, float…etc) are also objects. we can get the type of object by using type() function.
  Example:

                                  
                                      a = 10
                                      type(a) ->  class 'int' , gives the class type
                                  
                              

  Copy
• 2) We can convert one type to other type by using conversion function like int(), float(), str().. etc
• 3) Every object has an id. We can get the id of any object by using “id(object)”.
• 4) Python is also reference based. We need to use “id()” to check objects are pointing to same data. Example :

                                  
                                      a = 10
                                      b = 10
                                      if id(a) == id(b):    #checks if id of a is same as id of b
                                  
                              

  Copy
• 5) We can also override the predefined function to our requirement. We need to be careful whether we want it or not. Example:

                                      
                                          print(“Hello”)  #here print is a predefined  function
                                          print = 10 # here print is a int variable.
                                      
                                  

  Copy
• 6) If we want to restore the functionality of the print without restarting the session. One simple way is to delete the “print” variable using “del”. Example:

                              
                                  del print
                              
                          

  Copy
• 7) Initialize an list by using “[ ]” Example:

                              
                                  a = [] #empty list
                                  b = [1,2,3,4]
                              
                          

  Copy
• 8) Some basic operations on list:

                              
                                  a = [1,2,3,4,5,6]                #Initializing the list
                                  b = [[1,2,3],4,5,[6,7,8,]]     # nested list Initializing
                                  b = a                                # reference of a to b
                                  c = a.copy()                      #coping the list
                                  a.append(7)                      #appending the element
                                  a.extend([8,9,10,11])         #extend the list by appending another list
                              
                          

  Copy
  list Slicing:

                              
                                  a = [1,2,3,4,5,6,7,8,9]
                                  b = a[0:5:2]          # here 0 is start index
                                                                # 5 is end index
                                                                # 2, increment count
                                  now b will be having [1,3,5]
                                  we can use above step for copying the lists
                                  b = a[:]                  # we are not giving any arguments here, default it will take entire range
                                  # now b will have copy of the same list as a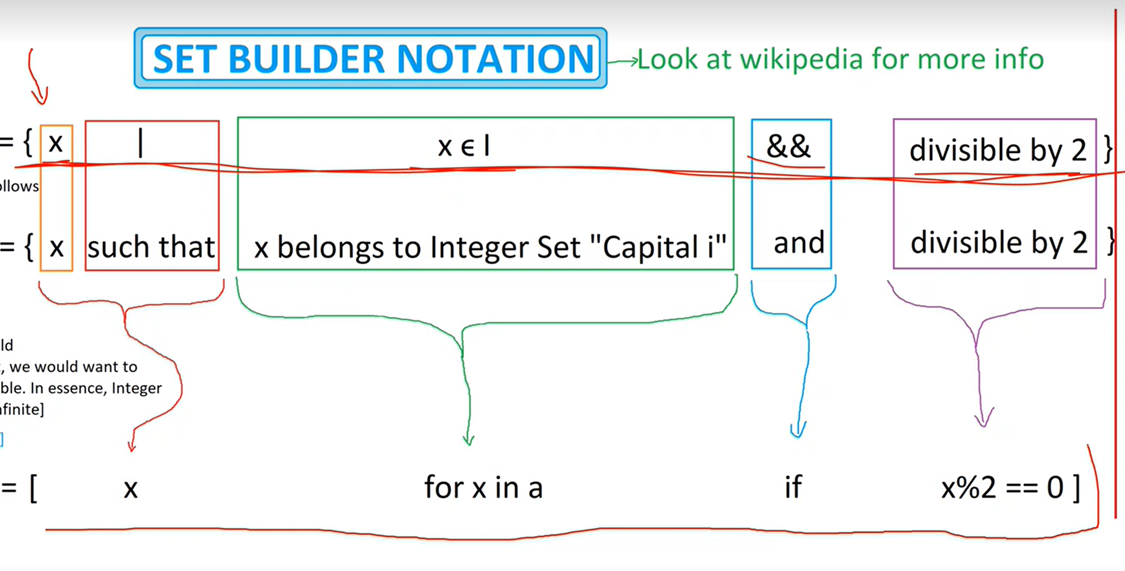
                              
                          

  Copy
  Set Builder notation:

  Example:

                              
                                  a = [1,2,3,4,5,6,7,8,9]
                                  b = [x for x in a]                               # here it will copy all the elements of a
                                  b -> [1,2,3,4,5,6,7,8,9]
                                  b = [x for x in a if x%2 == 0]          # here it will have even numbers of a. because of the condition.
                                  b -> [2,4,6,8]
                                  b = [2*x for x in a if x%2 == 0]      # here its same as above. But all even values will be doubled and placed in b
                                  b -> [4,8,12,16]                                
                              
                          

  Copy

  Refer the video for explanation

• 9) Adding Temp path variable in python:

                                  
                                      import sys
                                      sys.path -> gives the path data which is present in environment path in a list
                                      sys.path.append(“D:/pythonLibs”)             #adds the path given here to the python session. Which is temporary and limited to the session.
                                  
                              

  Copy
• 10) by default, there is a reserved python environment variable "PYTHONPATH". where we can add all the path locations, those will be included by default and we can use them by importing directly.

Assignment:

                            
                                with open(r"D:\temp\myTet.stl") as f:
                                p, area, vol = [],0, 0
                                for i in f.readlines():
                                    if 'normal' in i or 'vertex' in i:
                                        p.append([float(x) for x in i.split()[-3:]])
                                        if len(p)%4 == 0:
                                            n, v1, v2, v3 = p
                                            a = ((v1[0]-v2[0])**2+(v1[1]-v2[1])**2+(v1[2]-v2[2])**2)**0.5
                                            b = ((v1[0]-v3[0])**2+(v1[1]-v3[1])**2+(v1[2]-v3[2])**2)**0.5
                                            c = ((v3[0]-v2[0])**2+(v3[1]-v2[1])**2+(v3[2]-v2[2])**2)**0.5
                                            s = (a+b+c)/2.0
                                            ap = [sum(v)/3 for v in zip(v1, v2, v3)] # calculating centroid of the triangle
                                            da = (s * (s-a) * (s-b) * (s-c))**0.5 # small area
                                            area = area + da
                                            vol = vol + (ap[0]*n[0]+ap[1]*n[1]+ap[2]*n[2])*da/3 # gauss divergence theorem
                                                                                                # Field vector taken is xi + yj + zk, whose divergence is a scalar 3.
                                            p.clear()
                                print(area, vol)